Understanding Taleb’s convexity paper
Recommended by Daniel Vassallo, Understanding is a Poor Substitute for Convexity (Antifragility) is an excellent work by Taleb. It applies not just to science, but also to business and life (or any system that has a big “convexity bias”). I made this simplified version with the help of AI.
Disclaimer: This is just for my personal study. Please read the original paper by Nassim Nicholas Taleb here.
Historians have studied how scientific and technological discoveries have been made, but they have missed something very important. People have argued that luck is more important than a plan. But luck cannot be used to make a plan. The real reason for success is something called asymmetry (or convexity) of payoffs. Knowing about this special math can help give us rules and guidelines to help us make discoveries.
The story of luck versus knowledge is strange. We have more evidence for results that happen by luck than for those that happen because of plans. In some complicated and hard to understand areas like medicine or engineering, a plan does not work in most cases. This means we have come to where we are today mostly by accident, but we still use plans to try and make things happen in the future. We know that this is not quite right, but we do it anyway.
Technology and science have been able to improve over time, but it can’t be because of luck or making mistakes. Luck cannot lead to long term gains (otherwise it would not be chance); if we make mistakes, it won’t always work because planes can crash, buildings can collapse, and knowledge can get worse. So, the success must come from something else. That something is a special kind of exposure which is like a payoff function. That function has bigger gains than losses, and the math property of this asymmetry is convexity (see Figure 1). Convexity is like a special kind of option that can take advantage of uncertainty and messiness. This way, we can make rational, organized plans to make use of randomness and get good results.
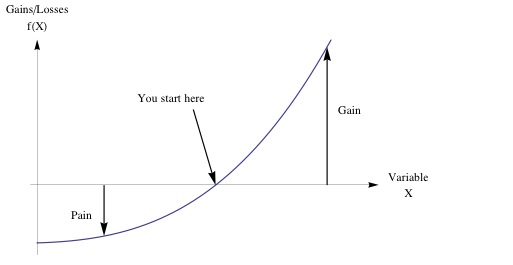
Further, when it comes to complicated systems, we often don’t know how things end up where they are. A great way to figure it out is by trying different things and seeing which one works best. An example of this is cooking. To make a dish, we might add an ingredient and then taste it to see if it tastes better. If we like it, we keep it. If not, we discard it. The important thing is that we have the option, not the obligation to keep the result. So we can enjoy gains without affected by the losses.
This “optionality” is important behind convexity. It means that you can get more benefits than drawbacks when you choose from different results and ignore the rest. This idea is like how evolution works - when something changes, it is only kept if it is better. People also choose what works best for them. Unlike nature which automatically chooses the best one, they do it intentionally, although people have mental biases and cultural problems that work against them. Optionality gives us the freedom to choose whatever we want. We don’t need to rely on making plans or predictions. (Just like when you go on a vacation to a place that has lots of things to do, you can plan what you’re going to do by asking a few questions before you go.)
While making a better recipe for hummus isn’t going to revolutionize the world, some discoveries have the potential to offer huge rewards. For example, penicillin, chemotherapy, and clean energy technologies can have a huge impact on the world (these are known as “Black Swans”). In the 1920s, people like Domagk conducted hundreds of trials using dyes to discover the first antimicrobial drugs, even though they didn’t really understand what was happening biologically. Unlike buying a financial option, where someone pays a fee, the rewards from research are not limited.
When we do research and try to figure out the best way to spend our money, we use math properties that have been around since the 1700s. Let’s call this “convexity bias”, which means that if something has a bigger chance of giving us a big benefit than it does of causing us harm, then it is better to do it. Two things are related: 1) the more convex the payoff function and 2) the more unpredictable the situation, the bigger the bias. People don’t like uncertainty, but don’t forget that it can be good for us.
The author gave the name “antifragile” to things that like a lot of change, chaos, and surprises. This is the opposite of a fragile thing which likes peace and calm. A coffee cup is an example of something fragile because it doesn’t like too much chaos. On the other hand, things that are antifragile like a lot of chaos because it helps them. When you add chaos and mistakes to an airplane ride, it makes things worse because it’s fragile or follows a concave function. But when you add chaos to research, it makes things better. Such convexity bias allows us to make rules to help us make smart decisions when things are chaotic.
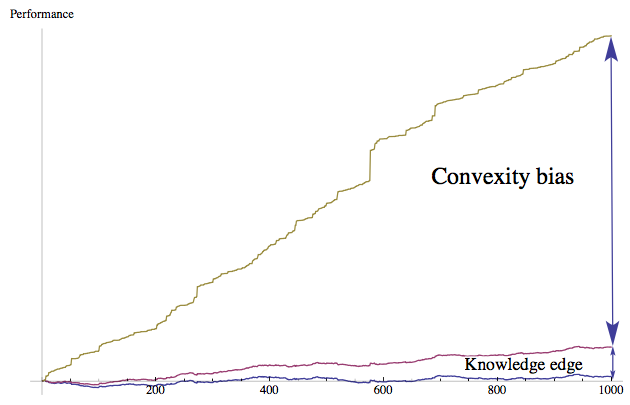
1) Convexity is easier to have than knowledge. As in figure 2, when we are not sure what we are looking for, it is better to try to make the payoff (the reward for doing something) better, instead of trying to find out exactly what we are looking for. We can make the payoff better by lowering the cost of trying different things.
2) It is better to try a lot of different things and spread out your efforts. Instead of putting all your eggs in one basket, divide your energy and resources across many different attempts. This way, you have a better chance of succeeding than if you only try one thing. Having a lot of small chances is better than having one big chance.
Sometimes when scientists do research, it can be like a game of chance. Very rarely, something amazing can happen that has a huge impact. For example, a single company might make up half of a country’s economy, and a single book might be the most popular in the world.
3) A chain of options. A rigid business plan is like a highway without exits - it doesn’t give you any options. To be successful, plans need to 1) give you lots of options with frequent ways out and 2) be short-term so you can make the most of the long-term. For example, five one-year options are worth much more than one five-year option.
4) Research without a plan or story. People in California who are trying to make money from new technologies often work with people they trust, instead of following a plan or narrative written on paper. Those people work together to try different ideas and keep trying until they find a successful one. Strategic planning usually doesn’t work.
5) We learn by experimenting rather than by thinking and understanding first. Textbooks often show that technology comes from science, but it is actually the other way around. For example, in the industrial revolution, there was not much evidence of science helping, but hobbyists tinkering around with things was the main cause. Figure 2 shows convexity is a kind of bias that can be found in random processes and it can be much better than having knowledge. Historical accounts of technology don’t usually mention convexity, but it is still important.
6) Simpler is better. The simplest inventions or technologies often get forgotten or ignored. It took five thousand years for people to think of putting wheels on suitcases after the wheel was invented. In real life, there is no reward or special recognition for making things more complicated. But in school or in research, people often look for complicated explanations and theories. If we look for stories, it tend to increase the complexity. In reality it is impossible to know ahead of time what knowledge you need to complete a task.
7) Keep track of what doesn’t work. When we learn about things that don’t work, it helps us narrow down what we can do. That’s why we need to pay attention to things that don’t work.
Some people have argued that the idea of research has similarities to buying lottery tickets. Lottery tickets are usually too expensive because people tend to pay too much for a chance to win something that is very unlikely to happen. But this comparison is wrong because lotteries are created and sold by humans and have a limit on how much can be won. Research has the potential to produce much bigger rewards, without limits. We have proof that banks don’t make money when they bet on something that has a low probability of success, which makes research the opposite of banking.
Thanks to the AI assistant from Readwise Reader to make this possible. Sign up with this link to get an extra free month.